梯度下降

简介

梯度：对于可微的数量场，以为分量的向量场称为f的梯度或斜量。

梯度下降法(gradient descent)是一个最优化算法，常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。

求解过程

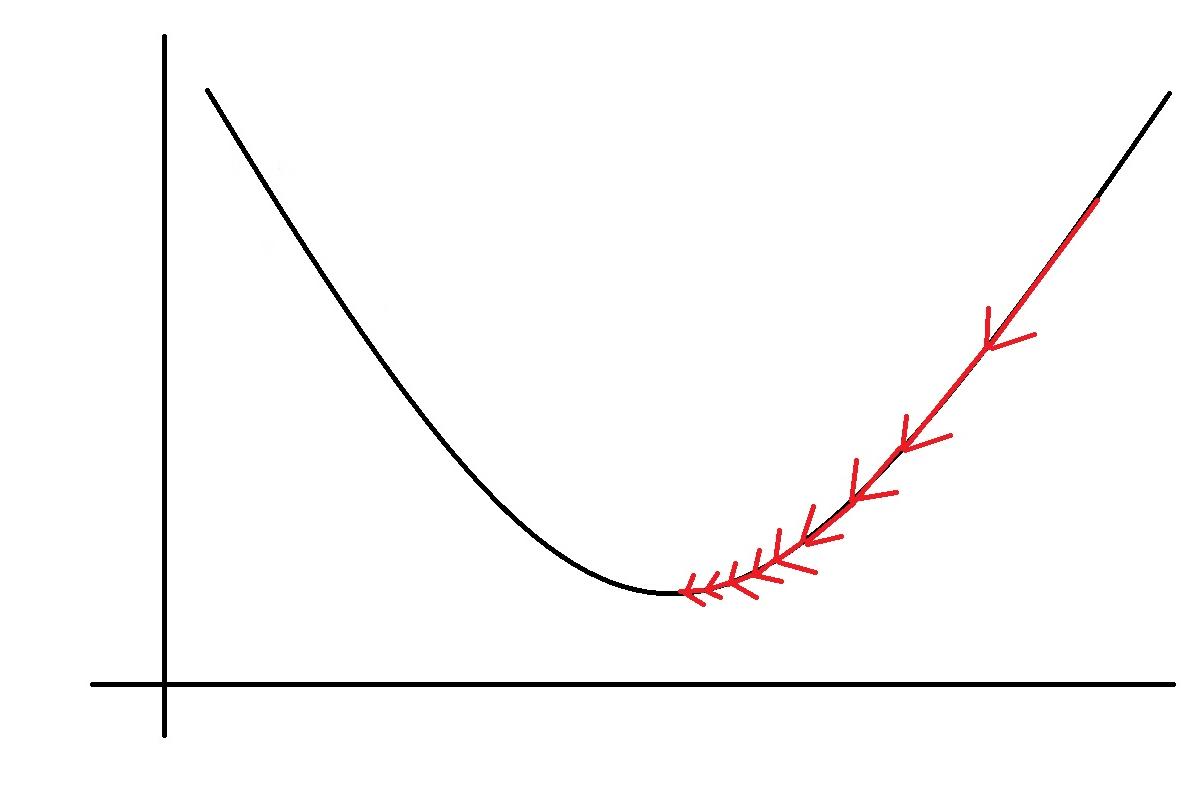
顾名思义，梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。

其迭代公式为 ，其中 代表梯度负方向， 表示梯度方向上的搜索步长。梯度方向我们可以通过对函数求导得到，步长的确定比较麻烦，太大了的话可能会发散，太小收敛速度又太慢。一般确定步长的方法是由线性搜索算法来确定，即把下一个点的坐标看做是ak+1的函数，然后求满足f(ak+1)的最小值的ak+1即可。

因为一般情况下，梯度向量为0的话说明是到了一个极值点，此时梯度的幅值也为0.而采用梯度下降算法进行最优化求解时，算法迭代的终止条件是梯度向量的幅值接近0即可，可以设置个非常小的常数阈值。

应用

举一个非常简单的例子，如求函数 的最小值。

利用梯度下降的方法解题步骤如下：

1、求梯度，

2、向梯度相反的方向移动 ，如下

 ，其中， 为步长。如果步长足够小，则可以保证每一次迭代都在减小，但可能导致收敛太慢，如果步长太大，则不能保证每一次迭代都减少，也不能保证收敛。

3、循环迭代步骤2，直到 的值变化到使得 在两次迭代之间的差值足够小，比如0.00000001，也就是说，直到两次迭代计算出来的  基本没有变化，则说明此时  已经达到局部最小值了。

4、此时，输出  ，这个  就是使得函数  最小时的  的取值 。

MATLAB如下。

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

%% 最速下降法图示

% 设置步长为0.1，f_change为改变前后的y值变化，仅设置了一个退出条件。

syms x;f=x^2;

step=0.1;x=2;k=0;         %设置步长,初始值,迭代记录数

f_change=x^2;             %初始化差值

f_current=x^2;            %计算当前函数值

ezplot(@(x,f)f-x.^2)       %画出函数图像

axis([-2,2,-0.2,3])       %固定坐标轴

hold on

while f_change>0.000000001                %设置条件，两次计算的值之差小于某个数，跳出循环

    x=x-step*2*x;                         %-2*x为梯度反方向，step为步长，！最速下降法！

    f_change = f_current - x^2;           %计算两次函数值之差

    f_current = x^2 ;                     %重新计算当前的函数值

    plot(x,f_current,'ro','markersize',7) %标记当前的位置

    drawnow;pause(0.2);

    k=k+1;

end

hold off

fprintf('在迭代%d次后找到函数最小值为%e，对应的x值为%en',k,x^2,x)

梯度下降法处理一些复杂的非线性函数会出现问题，如Rosenbrock函数：,其最小值在 处，函数值为 。但是此函数具有狭窄弯曲的山谷，最小点  就在这些山谷之中，并且谷底很平。优化过程是之字形的向极小值点靠近，速度非常缓慢。

缺点

靠近极小值时收敛速度减慢。

直线搜索时可能会产生一些问题。

可能会“之字形”地下降。