原理
第一抽屜原理
原理1:把多于n個的物體放到n個抽屜裡,則至少有一個抽屜裡的東西不少于兩件。n證明(反證法):如果每個抽屜至多隻能放進一個物體,那麼物體的總數至多是n×1,而不是題設的n+k(k≥1),故不可能。
n原理2:把多于mn(m乘n)+1(n不為0)個的物體放到n個抽屜裡,則至少有一個抽屜裡有不少于(m+1)的物體。n證明(反證法):若每個抽屜至多放進m個物體,那麼n個抽屜至多放進mn個物體,與題設不符,故不可能。
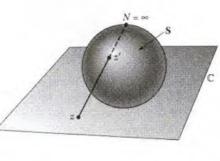
n原理3:把無數還多件物體放入n個抽屜,則至少有一個抽屜裡有無數個物體。n原理1、2、3都是第一抽屜原理的表述。n
第二抽屜原理
把(mn-1)個物體放入n個抽屜中,其中必有一個抽屜中至多有(m—1)個物體(例如,将3×5-1=14個物體放入5個抽屜中,則必定有一個抽屜中的物體數少于等于3-1=2)。
常見運用
構造抽屜的方法
運用抽屜原理的核心是分析清楚問題中,哪個是物件,哪個是抽屜。例如,屬相是有12個,那麼任意37個人中,至少有一個屬相是不少于4個人。這時将屬相看成12個抽屜,則一個抽屜中有37/12,即3餘1,餘數不考慮,而向上考慮取整數,所以這裡是3+1=4個人,但這裡需要注意的是,前面的餘數1和這裡加上的1是不一樣的。
因此,在問題中,較多的一方就是物件,較少的一方就是抽屜,比如上述問題中的屬相12個,就是對應抽屜,37個人就是對應物件,因為37相對12多。n
最差原則
最差原則,即考慮所有可能情況中,最不利于某件事情發生的情況。n例如,有300人到招聘會求職,其中軟件設計有100人,市場營銷有80人,财務管理有70人,人力資源管理有50人。那麼至少有多少人找到工作才能保證一定有70人找的工作專業相同呢?
此時我們考慮的最差情況為:軟件設計、市場營銷和财務管理各錄取69人,人力資源管理的50人全部錄取,則此時再錄取1人就能保證有70人找到的工作專業相同。因此至少需要69*3+50+1=258人。
根據第一抽屜原理之原理2推導:mn+1個人的時候必有m+1個人找到的工作專業相同,所以是要求出mn+1的人數,已知n=3,m+1=70。考慮到人力資源專業隻有50人,得出mn+1=(69*3+50)+1=258人。
一個抽屜裡有20件襯衫,其中4件是藍的,7件是灰的,9件是紅的,則應從中随意取出多少件才能保證有5件是同顔色的?
根據鴿巢原理,n個鴿巢,kn+1隻鴿子,則至少有一個鴿巢中有k+1隻鴿子。若根據鴿巢原理的推論直接求解,此時k=4,n=3,則應抽取3X4+1=13件才能保證有5件同色。其實不然,問題的模型和鴿巢原理不盡相同。在解決該問題時,應該考慮最差的情況,連續抽取過程中抽取出4件藍色的襯衣,即4件藍色,取走後,問題變成有灰色和紅色構成相同顔色的情況,這時,n=2,k+1=5,k=4.故應取4+4X2+1=13件。
問題分析:該情況下鴿巢原理的推論不再适用,由于藍色的襯衫隻有4件,而題目中要求有5件是同色的,導緻4件藍色襯衫都被抽取出這一最差情況的存在,所以應該先考慮最差情況,然後在此基礎上再運用鴿巢原理。n
證明
(反證法):若每個抽屜都有不少于m個物體,則總共至少有mn個物體,與題設矛盾,故不可能。
趣聞
已知n+1個互不相同的正整數,它們全都小于或等于2n,證明當中一定有兩個數是互質的。n匈牙利大數學家厄杜斯(PaulErdous,1913-1996)向當年年僅11歲的波薩(LouisPósa)提出這個問題,而小波薩思考了不足半分鐘便能給出正确的答案。
波薩是這樣考慮問題:取n個盒子,在第一個盒子我們放1和2,在第二個盒子我們放3和4,第三個盒子是放5和6,依此類推直到第n個盒子放2n-1和2n這兩個數。
如果我們在n個盒子裡随意抽出n+1個數。我們馬上看到一定有一個盒子是被抽空的。因此在這n+1個數中必有兩個數是連續數,很明顯的連續數是互質的。因此這問題就解決了!這就是利用了鴿巢原理的核心思想。