原理
第一抽屉原理
原理1:把多于n个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。n证明(反证法):如果每个抽屉至多只能放进一个物体,那么物体的总数至多是n×1,而不是题设的n+k(k≥1),故不可能。
n原理2:把多于mn(m乘n)+1(n不为0)个的物体放到n个抽屉里,则至少有一个抽屉里有不少于(m+1)的物体。n证明(反证法):若每个抽屉至多放进m个物体,那么n个抽屉至多放进mn个物体,与题设不符,故不可能。
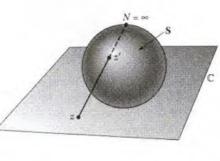
n原理3:把无数还多件物体放入n个抽屉,则至少有一个抽屉里有无数个物体。n原理1、2、3都是第一抽屉原理的表述。n
第二抽屉原理
把(mn-1)个物体放入n个抽屉中,其中必有一个抽屉中至多有(m—1)个物体(例如,将3×5-1=14个物体放入5个抽屉中,则必定有一个抽屉中的物体数少于等于3-1=2)。
常见运用
构造抽屉的方法
运用抽屉原理的核心是分析清楚问题中,哪个是物件,哪个是抽屉。例如,属相是有12个,那么任意37个人中,至少有一个属相是不少于4个人。这时将属相看成12个抽屉,则一个抽屉中有37/12,即3余1,余数不考虑,而向上考虑取整数,所以这里是3+1=4个人,但这里需要注意的是,前面的余数1和这里加上的1是不一样的。
因此,在问题中,较多的一方就是物件,较少的一方就是抽屉,比如上述问题中的属相12个,就是对应抽屉,37个人就是对应物件,因为37相对12多。n
最差原则
最差原则,即考虑所有可能情况中,最不利于某件事情发生的情况。n例如,有300人到招聘会求职,其中软件设计有100人,市场营销有80人,财务管理有70人,人力资源管理有50人。那么至少有多少人找到工作才能保证一定有70人找的工作专业相同呢?
此时我们考虑的最差情况为:软件设计、市场营销和财务管理各录取69人,人力资源管理的50人全部录取,则此时再录取1人就能保证有70人找到的工作专业相同。因此至少需要69*3+50+1=258人。
根据第一抽屉原理之原理2推导:mn+1个人的时候必有m+1个人找到的工作专业相同,所以是要求出mn+1的人数,已知n=3,m+1=70。考虑到人力资源专业只有50人,得出mn+1=(69*3+50)+1=258人。
一个抽屉里有20件衬衫,其中4件是蓝的,7件是灰的,9件是红的,则应从中随意取出多少件才能保证有5件是同颜色的?
根据鸽巢原理,n个鸽巢,kn+1只鸽子,则至少有一个鸽巢中有k+1只鸽子。若根据鸽巢原理的推论直接求解,此时k=4,n=3,则应抽取3X4+1=13件才能保证有5件同色。其实不然,问题的模型和鸽巢原理不尽相同。在解决该问题时,应该考虑最差的情况,连续抽取过程中抽取出4件蓝色的衬衣,即4件蓝色,取走后,问题变成有灰色和红色构成相同颜色的情况,这时,n=2,k+1=5,k=4.故应取4+4X2+1=13件。
问题分析:该情况下鸽巢原理的推论不再适用,由于蓝色的衬衫只有4件,而题目中要求有5件是同色的,导致4件蓝色衬衫都被抽取出这一最差情况的存在,所以应该先考虑最差情况,然后在此基础上再运用鸽巢原理。n
证明
(反证法):若每个抽屉都有不少于m个物体,则总共至少有mn个物体,与题设矛盾,故不可能。
趣闻
已知n+1个互不相同的正整数,它们全都小于或等于2n,证明当中一定有两个数是互质的。n匈牙利大数学家厄杜斯(PaulErdous,1913-1996)向当年年仅11岁的波萨(LouisPósa)提出这个问题,而小波萨思考了不足半分钟便能给出正确的答案。
波萨是这样考虑问题:取n个盒子,在第一个盒子我们放1和2,在第二个盒子我们放3和4,第三个盒子是放5和6,依此类推直到第n个盒子放2n-1和2n这两个数。
如果我们在n个盒子里随意抽出n+1个数。我们马上看到一定有一个盒子是被抽空的。因此在这n+1个数中必有两个数是连续数,很明显的连续数是互质的。因此这问题就解决了!这就是利用了鸽巢原理的核心思想。