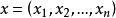置换群

简介

一类具体的有限群。有限集合到自身的一一映射称为一个置换。有限集合Ω上的一些置换组成的集合，在置换的乘法下所组成的群，称为置换群。此群的阶是有限的。研究置换群的性质和构造的理论称为置换群论。凯莱(Cayley，A.)证明：任何一个有限群都同构于一个置换群。因此，可以把一切有限群都看成置换群。由于置换群比抽象群更为直观，而一些数学对象的自同构群是以置换群的面貌出现的，所以，在历史上对置换群的研究先于对抽象群的研究。著名的伽罗瓦理论就是把高次方程的根式可解性的研究转化成为对置换群的研究的，事实上，伽罗瓦(Galois，E.)本人就曾得到有关置换群的一些深刻定理。

置换群

置换群

置换群

置换群

置换群

其中 是 的一个排列，是 在置换 下的像。由全排列知识可知，这样的置换共有 个。

置换群

置换群

置换群

置换群

有时也把 在 下的像记为。根据映射的乘法可以定义Ω上任意两个置换 与 的乘积 为

对于这样定义的运算，Ω上全体置换所组成的集合Sω成一个群，称为Ω上的对称群或n元对称群，简称对称群，其阶为 n!。对称群的子群称为Ω上的置换群或简称置换群。当 时把Sω 记为Sn。较置换群更为一般的概念，有所谓的作用。

作用

G是一个群，Ω是一个非空集合。G中每个元素g都对应Ω的一个映射：x→xg，x∈Ω，若满足：

②xe=x（e是G的单位元素）

则称G作用于Ω上。G作用于Ω上的充分必要条件是，G同态于Ω上的一个置换群。

设G是Ω上的一个置换群，H是Γ上的一个置换群。如果存在Ω到Γ上的一个一一对应ρ，以及G到H上的一个一一对应φ,使得对Ω中任一个点α及G中任一个置换g都有

如果 Ω与Γ都是n元集合，那么Sω与Sг是置换同构的。因此，n元对称群都与Sn置换同构。

基本性质

b. 可结合性

置换群

=

c. 单位元

重要定理

定理1 不相连轮换相乘时可以交换

定理2 每个（非轮换）的置换都可表为不相连轮换之积；每个轮换都可表为对换之积，因此，每个置换都可表为对换之积

定理3 每个置换表成对换的乘积时，其对换个数的奇偶性不变

轮换对换

任一置换都可表为一些对换的乘积，表示法不是唯一的，但是表示式中对换个数的奇偶是唯一确定的。若σ可表成偶数个对换的乘积，则称σ为偶置换。若σ可表成奇数个对换的乘积，则称σ为奇置换。

Sω中全部偶置换组成Sω的一个正规子群，称为n元交错群，简称交错群，记作Aω。Sn的交错子群记作An。n元交错群都与An置换同构。当n≥2时,An的阶为n!/2。当n≠4时，An是单群，这是一类很重要的有限单群。

置换群是有限群的一类重要例子，有限群的研究是从置换群开始的。置换群的重要性还在于下述事实。

凯莱定理（Cayley's theorem）

任一有限群都与其元素的一个置换群同构。

区及轨道 设G是Ω上一个置换群，墹是Ω的一个子集，g是G中任一元素，用墹g表示墹在g下的像集

。若对于G中任一元素 g都有墹g=墹，或

，则称墹是一个区。空集═以及Ω都是区，称为平凡区。其余的区称为非平凡区。两个区的交仍是区。

若对G中任一元素g，都有墹g=墹，则称 墹是G的一个不变区。Ω及═都是不变区。不变区的交仍是不变区。

设墹是G的一个不变区，如果对墹中任意两个点α、β都有G中一个元素g使得αg=β，那么墹称为G 的一个轨道（或传递集）。如果墹是G 的一个轨道，那么，任取墹中一个点α，都有

。而且，G 的任一个轨道都可这样得到。如果墹及Γ是G 的两个轨道，那么墹=Г 或墹∩Г=═。因此,Ω分成G 的一些两两不交的轨道之并。轨道中元素的个数称为轨道的长度。

稳定子群

设G是一个n元置换群，作用于Ω上。取定Ω中一个点α

,是G 的一个子群，称为G 对α 的稳定子群。如果

，并设

(通常取恒等置换作为g1)，那么

。因此,|G|=|Gα||αG|，所以G 的轨道的长度一定能整除G 的阶。

如果对任一α∈Ω，都有Gα={e}，则称G是半正则群。此时，G的任一轨道长都等于|G|。

稳定子群的概念还可以推广到多个点的情形。取定Ω中k个点α1,α2,…,αk,则是G的一个子群，称为G对α1,α2,…,αk的稳定子群。显然有。

传递性

设G是Ω上一个置换群。若对任意α,β∈Ω，都可找到g∈G,使得αg=β,则称G在Ω上是传递的；否则，称G是非传递的。G是传递群当且仅当Ω是 G的一个轨道。因此，若G是传递群，则|Ω|是|G|的一个因子。若G是传递群，且|Ω|=|G|,则称G是一个正则群。正则群就是传递的半正则群。

若在一个非正则传递群G中，每个非单位元素最多保持一个文字不变，则G 称为弗罗贝尼乌斯群。在弗罗贝尼乌斯群G中，没有不变文字的置换与恒等置换一起构成一个正则群R，R是G 的一个特征子群。

若对于Ω中任意两个k元有序点组α1，α2,…,αk及β1,β2,…,βk,都有G中一个置换g使

，则称G是一个 k重传递群或 k传递群。k重传递群一定是(k-1)重传递的。如果k≥2，那么k重传递群称为多重传递群，否则称为单传递群。如果G是Ω上一个传递群，那么当且仅当Gα在Ω-{α}上(K-1)重传递群时,G是k重传递的。k重传递的n元置换群G 的阶可被n(n-1)…(n-k+1)整除。若G 的阶恰等于n(n-1)…(n-k+1),则称G是一个精确 k重传递群。此时，对于Ω中任意两个k元点组α1,α2,…,αk;β1,β2,…,βk,在G中恰有一个g使α=βi,i=1，2，…，k。

对称群Sn是 n重传递的，交错群An是n-2重传递的。除去Sn及An外，有无穷多个3重传递群，但是只知道4个4重传递群，它们是法国数学家 É.L.马蒂厄在1861年及1873年先后发现的次数分别为11，12，23及24的马蒂厄群M11,M12,M23,M24，其中M12及M24是5重传递的，而且M11是M12的稳定子群，M23是M24的稳定子群，它们的阶分别是M11及M12都是精确传递群。

公式

在1981年有限单群分类的问题解决以后，所有双重传递群已被决定，并且知道没有传递重数大于或等于6的传递单群，而交错群与上述4个马蒂厄群是仅有的4重传递的单置换群。M23的稳定子群是M22,也是一个单群，这5 个马蒂厄群是最早发现的不属于有限单群的无穷系列的5个零散单群。

置换群的循环表示

循环

置换群

置换群

置换群

约定 为一个m阶的循环表示，其表示为将 替换为，将 替换为，......，将 替换为，将 替换为。(a1a2…am)=(a2a3…ama1)=…=(ama1…am-1)有m种表示方法。

若两个循环无共同文字，称为不相交的，不相交的循环相乘可交换。

循环表示

置换群

置换群

置换群

置换群

置换群

置换群

1→ → →…→ →1得一循环(1 … ),

置换群

置换群

置换群

若(1 … )包含了[1,n]的所有文字，则命题成立。

否则在余下的文字中选一个，继续搜索，又得一循环。直到所有文字都属于某一循环为止。

因不相交循环可交换，故除了各个循环的顺序外，任一置换都有唯一的循环表示。

2阶循环(i,j)叫做对换，任意一个循环都能表达成若干换位之积。任意一个循环分解为若干之积不是唯一的，甚至与连换位的数目都不相同。例如(12 …n)=(23)(2 4)…(2 n)(2 1)，(12 3) = (12)(13) = (12)(13)(31)(13)。但是有一个性质是不变的，即换位数目的奇偶性不变。即一个置换分解为若干个数目的置换之积，可分解成奇数个换位之积的置换，不可能表示为偶数个换位之积；反之，也成立。证明如下：

设l,k(l正整数常数，则有

若将l和k换位，(l k)f =-f

每次对换都改变f的符号，则对应的分解的奇偶性是唯一的。

奇循环与偶循环

置换分成两大类：奇置换与偶置换。

若一个置换能分解为奇数个换位之积，则为奇置换，若可以分解为偶数个换位之积，则为偶置换。

S= (1)(25)(37)(46) 3个换位，奇置换

置换群

例右图中0表示空格，有些布局通过左图偶数次换位得到，有些是奇数次换位得到，但奇数次换位得到的不能通过偶数次换位来得到。如果限制任一变动都是与0做相邻的对换，是否能够由左图生成右图？

显然0从右下角出发回到右下角，水平方向上，垂直方向上都做了偶数次对换。一个奇置换不会等于一个偶置换。

[1,n]上的所有置换(共n!个)构成一个群，称为n阶对称群(Symmetricgroup)，记做Sn.

定理： Sn中所有偶置换构成一阶为(n!)/2的子群称为交错群，记做An.

(1)封闭性：偶置换相乘还是偶置换

(2)结合律：置换群的结合律

(3)单位元：置换群的单位元素本身就是偶置换

(4)逆元 =

置换群

置换群

置换群

设 p =( )( )…( ),则p-1 = ( )…( )

故An为群

令Bn=Sn-An,|Bn|+|An|=n!,

置换群

置换群

秩

设G是Ω上的一个传递置换群，α∈Ω，G对α的稳定子群Gα作为Ω上的置换群，其轨道（包括平凡轨道{α}）数称为G的秩。显然，当且仅当G的秩等于2时,G是双传递的。秩为 3的单传递群是一类很重要的单传递群，在26个零散单群中，有8个是作为秩是3的置换群构造出来的群。

本原性 　设G是Ω上一个传递群，若G没有非平凡区，则称G是一个本原群，否则称为非本原群。多重传递群一定是本原群,Ω上传递群G是本原群的充分必要条件为其稳定子群Gα(α∈Ω)是G的极大子群。如果Ω上一个置换群G是k重传递的，并且对k-1个点的稳定子群在其余的点上是本原的，那么G称为k重本原的。

传递性、半传递

比k重传递性较弱的一个概念是k重集传递性。设G是Ω上一个置换群，若对于Ω的任意两个k元子集Δ、Γ都可找到 G中一个元素g 使得Δg=Γ,则称G是k重集传递的。传递性的另一个推广是所谓半传递性，若G的轨道长都相等且大于1,则G称为半传递的，或重传递的。

置换群的一个古老而有意义的问题，是找出全部互不置换同构的置换群。至今，已找出次数小于或等于11的全部置换群。所谓置换群的次数，即这个置换群所有实际变动的点的个数。当12≤n≤15时找出了全部n次传递群。而当n较大时，仅对n≤50找出了全部n次本原群。

常见的置换群

S={(1)、(1 2)}

S={(1)、(1 2)、(1 3)、(2 3)、(1 2 3)、(1 3 2)}

S={(1)、(1 2)、(1 3)、(1 4)、(2 3)、(2 4)、(3 4)、(1 2 3)、(1 3 2)、(1 2 4)、(1 4 2)、(1 3 4)、(1 4 3)、(2 3 4)、(2 4 3)、(1 2 3 4)、(1 2 4 3)、(1 3 2 4)、(1 3 4 2)、(1 4 2 3)、(1 4 3 2)、(1 2)(3 4)、(1 3)(2 4)、(1 4)(2 3)}