发现
欧拉回路是数学家欧拉在研究著名的德国哥尼斯堡(Koenigsberg)七桥问题时发现的。如图1所示,流经哥尼斯堡的普雷格尔河中有两个岛,两个岛与两岸共4处陆地通过7座杨彼此相联。7桥问题就是如何能从任一处陆地出发,经过且经过每个桥一次后回到原出发点。
这个问题可抽象为一个如图2所示的数学意义上的图,其中4个结点分别表示与4块陆土Il对应,如结点C对应河岸C,结点A对应岛A等,而结点之间的边表示7座桥。
欧拉由此提出了著名的欧拉定理。
1)欧拉路:通过图中所有边的简单路。
2)欧拉回路:闭合的欧拉路。
3)欧拉图:包含欧拉回路的图。
判断
以下判断基于此图的基图连通。
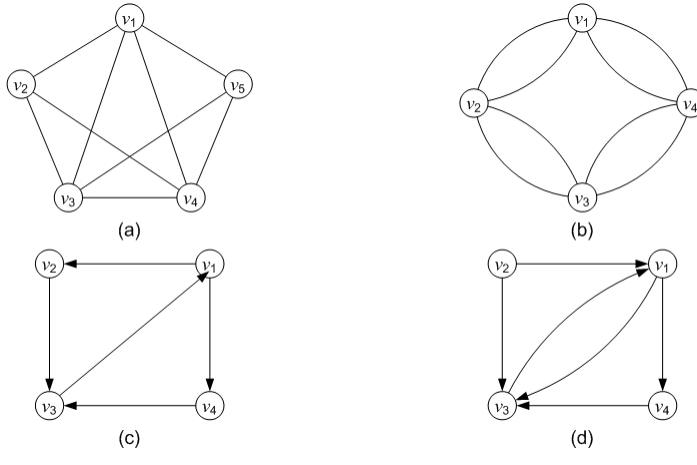
无向图存在欧拉回路的充要条件
一个无向图存在欧拉回路,当且仅当该图所有顶点度数都为偶数,且该图是连通图。
有向图存在欧拉回路的充要条件
一个有向图存在欧拉回路,所有顶点的入度等于出度且该图是连通图。
混合图存在欧拉回路条件
要判断一个混合图G(V,E)(既有有向边又有无向边)是欧拉图,方法如下:
假设有一张图有向图G',在不论方向的情况下它与G同构。并且G'包含了G的所有有向边。那么如果存在一个图G'使得G'存在欧拉回路,那么G就存在欧拉回路。
其思路就将混合图转换成有向图判断。实现的时候,我们使用网络流的模型。现任意构造一个G'。用Ii表示第i个点的入度,Oi表示第i个点的出度。如果存在一个点k,|Ok-Ik|mod 2=1,那么G不存在欧拉回路。
接下来则对于所有Ii>Oi的点从源点连到i一条容量为(Ii-Oi)/2的边,对于所有Ii
解法
无向图欧拉回路解法
求欧拉回路的一种解法
下面是无向图的欧拉回路输出代码:注意输出的前提是已经判断图确实是欧拉回路。
C语言代码,不全,请不要直接粘贴。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int num=0;//标记输出队列
int match[MAX];//标志节点的度,无向图,不区分入度和出度
void solve(int x)
{
if (match[x]==0)
Record[num++]=x;
else
{
for(int k=0;k<=500;k++)
{
if(Array[x][k]!=0)
{
Array[x][k]--;
Array[k][x]--;
match[x]--;
match[k]--;
solve(k);
}
}
Record[num++]=x;
}
}
|
pascal代码:
求无向图的欧拉回路(递归实现)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
program euler;
const maxn=10000;{顶点数上限}
maxm=100000;{边数上限}
typetnode=^tr;
tr=record
f,t:longint;{边的起始点和终止点}
al:boolean;{访问标记}
rev,next:tnode;{反向边和邻接表中的下一条边}
end;
varn,m,bl:longint;{顶点数,边数,基图的极大连通子图个数}
tot:longint;
g:array[1..maxn]oftnode;
d:array[1..maxn]oflongint;{顶点的度}
fa,rank:array[1..maxn]oflongint;{并查集中元素父结点和启发函数值}
list:array[1..maxm]oftnode;{最终找到的欧拉回路}
o:boolean;{原图中是否存在欧拉回路}
procedurebuild(ta,tb:longint);{在邻接表中建立边(ta,tb)}
vart1,t2:tnode;
begin
t1:=new(tnode);
t2:=new(tnode);
t1^.f:=ta;
t1^.t:=tb;
t1^.al:=false;
t1^.rev:=t2;
t1^.next:=g[ta];
g[ta]:=t1;
t2^.f:=tb;
t2^.t:=ta;
t2^.al:=false;
t2^.rev:=t1;
t2^.next:=g[tb];
g[tb]:=t2;
end;
proceduremerge(a,b:longint);{在并查集中将a,b两元素合并}
varoa,ob:longint;
begin
oa:=a;
whilefa[a]<>adoa:=fa[a];
fa[oa]:=a;
ob:=b;
whilefa[b]<>bdob:=fa[b];
fa[ob]:=b;
ifa<>bthenbegin
dec(bl);{合并后,基图的极大连通子图个数减少1}
ifrank[a]=rank[b]theninc(rank[a]);
ifrank[a]>rank[b]thenfa[b]:=aelsefa[a]:=b;
end;
end;
procedureinit;{初始化}
vari,ta,tb:longint;
begin
fillchar(fa,sizeof(fa),0);
fillchar(rank,sizeof(rank),0);
fillchar(d,sizeof(d),0);
readln(n,m);
fori:=1tondofa[i]:=i;
bl:=n;
fori:=1tomdobegin
readln(ta,tb);
build(ta,tb);
inc(d[tb]);
inc(d[ta]);
merge(ta,tb);
end;
end;
proceduresearch(i:longint);{以i为出发点寻找欧拉回路}
varte:tnode;
begin
te:=g[i];
whilete<>nildobegin
ifnotte^.althenbegin
te^.al:=true;
te^.rev^.al:=true;
search(te^.t);
list[tot]:=te;
dec(tot);
end;
te:=te^.next;
end;
end;
proceduremain;{主过程}
vari:longint;
begin
o:=false;
fori:=1tondo
ifd[i]=0thendec(bl);{排除孤立点的影响}
ifbl<>1thenexit;{原图不连通,无解}
fori:=1tondo
ifodd(d[i])thenexit;{存在奇点,无解}
o:=true;
fori:=1tondo
ifd[i]<>0thenbreak;
tot:=m;
search(i);{从一个非孤立点开始寻找欧拉回路}
end;
procedureprint;{输出结果}
vari:longint;
begin
ifnotothenwriteln('Nosolution.')elsebegin
writeln(list[1]^.f);
fori:=1tomdowriteln(list[i]^.t);
end;
end;
begin
init;
main;
print;
end.
|
注意record中的点的排列是输出的倒序,因此,如果要输出欧拉路径,需要将record倒过来输出。
求欧拉回路的思路:
循环的找到出发点。从某个节点开始,然后查出一个从这个出发回到这个点的环路径。这种方法不保证每个边都被遍历。
如果有某个点的边没有被遍历就让这个点为起点,这条边为起始边,把它和当前的环衔接上。这样直至所有的边都被遍历。这样,整个图就被连接到一起了。
具体步骤:
1。如果此时与该点无相连的点,那么就加入路径中
2。如果该点有相连的点,那么就加入队列之中,遍历这些点,直到没有相连的点。
3。处理当前的点,删除走过的这条边,并在其相邻的点上进行同样的操作,并把删除的点加入到路径中去。
4。这个其实是个递归过程。
相关词条
相关搜索
其它词条