加減法
加法法則
複數的加法按照以下規定的法則進行:設z1=a+bi,z2=c+di是任意兩個複數,
則它們的和是(a+bi)+(c+di)=(a+c)+(b+d)i。
兩個複數的和依然是複數,它的實部是原來兩個複數實部的和,它的虛部是原來兩個虛部的和。
複數的加法滿足交換律和結合律,
即對任意複數z1,z2,z3,有:z1+z2=z2+z1;(z1+z2)+z3=z1+(z2+z3)。
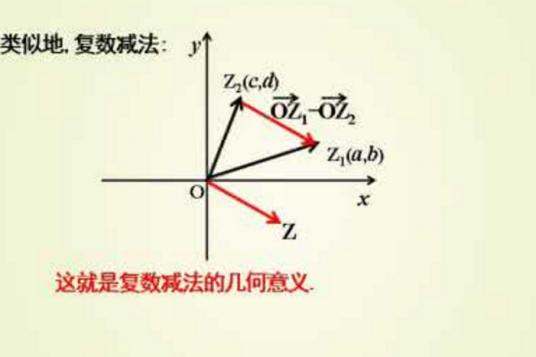
減法法則
複數的減法按照以下規定的法則進行:設z1=a+bi,z2=c+di是任意兩個複數,
則它們的差是(a+bi)-(c+di)=(a-c)+(b-d)i。
兩個複數的差依然是複數,它的實部是原來兩個複數實部的差,它的虛部是原來兩個虛部的差。
乘除法
乘法法則
規定複數的乘法按照以下的法則進行:
設z1=a+bi,z2=c+di(a、b、c、d∈R)是任意兩個複數,那麼它們的積(a+bi)(c+di)=(ac-bd)+(bc+ad)i。
其實就是把兩個複數相乘,類似兩個多項式相乘,展開得:ac+adi+bci+bdi2,因為i2=-1,所以結果是(ac-bd)+(bc+ad)i。兩個複數的積仍然是一個複數。
在極坐标下,複數可用模長r與幅角θ表示為(r,θ)。對于複數a+bi,r=√(a²+b²),θ=arctan(b/a)。此時,複數相乘表現為幅角相加,模長相乘。
除法法則
複數除法定義:滿足(c+di)(x+yi)=(a+bi)的複數x+yi(x,y∈R)叫複數a+bi除以複數c+di的商。
運算方法:可以把除法換算成乘法做,在分子分母同時乘上分母的共轭。所謂共轭你可以理解為加減号的變換,互為共轭的兩個複數相乘是個實常數。
除法運算規則:
①設複數a+bi(a,b∈R),除以c+di(c,d∈R),其商為x+yi(x,y∈R),
即(a+bi)÷(c+di)=x+yi
∵(x+yi)(c+di)=(cx-dy)+(dx+cy)i
∴(cx-dy)+(dx+cy)i=a+bi
由複數相等定義可知cx-dy=adx+cy=b
解這個方程組,得x=(ac+bd)/(c2+d2)y=(bc-ad)/(c2+d2)
于是有:(a+bi)/(c+di)=(ac+bd)/(c2+d2)+((bc-ad)/(c2+d2))i
②利用共轭複數将分母實數化得(見圖1):
點評:①是常規方法;②是利用初中我們學習的化簡無理分式時,都是采用的分母有理化思想方法,而複數c+di與複數c-di,相當于我們初中學習的的對偶式,它們之積為1是有理數,而(c+di)·(c-di)=c2+d2是正實數.所以可以分母實數化。把這種方法叫做分母實數化法。
另外,由上述乘法法則可得另一計算方法,即幅角相減,模長相除。
對數運算法則
對于複數(r,θ),有ln(r,θ)=lnr+iθ。
其他結論可由換底公式得到。
指數運算法則
由歐拉公式推得複數指數的ea+bi結果仍為複數,其幅角即為複數虛部b,其模長為ea。
對于複底數、實指數幂(r,θ)x,其結果為(rx,θ·x)。
對于複底數、複指數的幂,可用(a+bi)c+di=eln(a+bi)(c+di)來計算。