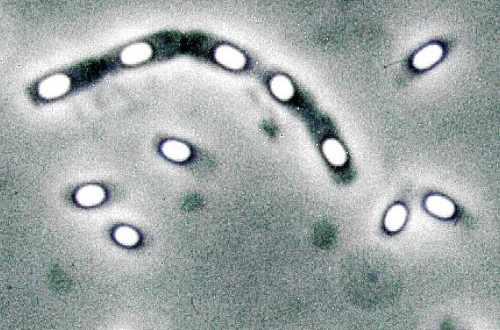
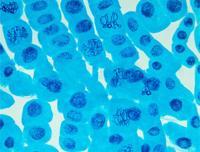
簡介
對任意複數s,若
,則: 這一信息在隔了漫長的122年之後終于被 Bernhard Riemann (1826 - 1866) 所破譯,于是便有了Riemann 的著名論文«論小于給定數值的素數個數»。Euler 乘積公式的證明十分簡單,唯一要小心的就是對無窮級數和無窮乘積的處理,不能随意使用有限級數和乘積的性質。我們在下面證明的是一個更為普遍的結果,Euler乘積公式将作為該結果的一個特例出現。
廣義歐拉乘積公式:設 f(n) 滿足
,且 ,則:證明
證明:由于
,因此 絕對收斂。考慮連乘積中 的部分 (有限項),由于級數絕對收斂,乘積又隻有有限項,因此可以使用與普通有限求和及乘積一樣的結合律及分配律。利用 f(n) 的乘積性質可得:其中右端求和對所有隻含 N 以下素數因子的自然數進行 (每個這樣的自然數隻在求和中出現一次,因為自然數的素數分解是唯一的)。由于所有本身在 N 以下的自然數顯然都隻含 N 以下的素數因子,因此,其中R(N)為對所有大于等于 N 但隻含 N 以下素數因子的自然數求和的結果。由此我們得到:要使廣義 Euler 乘積公式成立,隻需證明 即可。後者是顯然的,因為 ,而 表明 ,從而。由于
,因此廣義 Euler 乘積公式也可以寫成:在廣義 Euler 乘積公式中取 ,則顯然 對應于 Euler 乘積公式中的條件 ,而廣義 Euler 乘積公式退化為 Euler 乘積公式。從上述證明中我們可以看到, Euler 乘積公式成立的關鍵在于每一個自然數都具有唯一素數分解式這一基本性質 (即所謂的算術基本定理)。
Euler 本人的證明:除了上述證明方法外, Euler 原始論文中的證明方法也相當簡潔,值得介紹一下。仍以廣義 Euler 乘積公式為框架,注意到 (利用 f(n) 的性質):
因此:等式右端所有含有因子 2 的 f(n) 項都消去了 (這種逐項對消有賴于,即 絕對收斂)。類似地,以
乘以上式則右端所有含有因子 3 的 f(n) 項也都消去了,依此類推,将所有 (p 為素數) 乘上後右端便隻剩下了 f(1),即:其中最後一步再次使用了 f(n) 的性質 ()。将無窮乘積移到等式右邊顯然就得到了廣義 Euler 乘積公式。有興趣的朋友不妨試着将上述最後幾步用極限的語言嚴格表述一下。推論: Riemann ζ函數ζ(s)在
沒有零點。證明:設
,則 Euler 乘積公式給出:注意到對于任何 ,因此由上式可進一步推得:其中最後一步是因為對于 收斂。