基本介紹
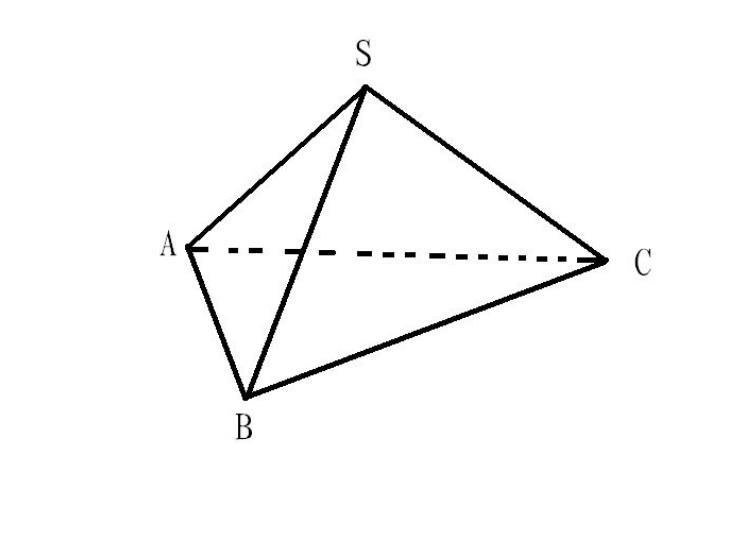
空間四邊形亦稱偏斜四邊形,是空間多邊形的一種,即各邊不在同一平面内的四邊形。若封閉折線ABCD為空間四邊形,則點A,B,C,D不在同一平面内,稱為空間四邊形的頂點.AB,BC,CD,DA稱為它的邊:其中AB,BC;BC,CD;CD,DA;DA,AB是它的四對鄰邊;AB,CD;BC,DA,是它的兩對對邊(如圖1)。AC與BD稱為它的對角線。連結對邊中點的線段稱為它的雙中位線。設P,Q,R,S分别是AB,BC,CD,DA的中點,則PR,QS是空間四邊形的兩條雙中位線。
性質
空間四邊形有下列性質:
1.連結兩對兩鄰邊中點的線段互相平行且相等,且都等于與之平行的對角線的一半。如圖2,
即:
因此,四邊中點組成一個平行四邊形.從而知空間四邊形的兩條雙中位線(PR與QS)相交且互相平分。
2.由于每三條依次相鄰的邊的中點都不在同一直線上.是三角形的頂點,可知一條雙中位線的長小于兩對角線的和的一半,即
PR
QS
3.若兩對角線互相垂直,則四邊形中點連線所成的平行四邊形為矩形。
4.取四邊形的ABCD的邊AB,BC,CD,DA的中心P,Q,R,S與對角線AC,BD的中點U,V,得到它的兩個平面PVRU與QUSV,第一個面是與對邊BC,DA平行的,第二個面是與對邊AB,CD平行的.人們把平行于空間四邊形一對對邊的平面稱為空間四邊形的方向平面。任一空間四邊形有兩組方向平面,每組中的平面相互平行。
5.若空間四邊形中,對邊中點的連線垂直且平分對邊時(如圖2中的PR或QS),則稱其為等腰偏斜梯形,且這對對邊中點的連線稱為等腰偏斜梯形的對稱軸
對角線
對角線,幾何學名詞,定義為連接多邊形任意兩個不相鄰頂點的線段,或者連接多面體任意兩個不在同一面上的頂點的線段。
例題解析
【例1】試證内接于空間四邊形的任何平面四邊形的對邊如果相交,那麼交點必定在空間四邊形的對角線上。
已知:如圖,空間四邊形ABCD,又平面四邊形PQRS的頂點P、Q、R、S分别在線段AB、AD、CD、CB上,且PQ∩SR=K。
求證:K∈BD。
證明∵P∈AB,Q∈AD,K∈PQ,
∴PQ⊂平面ABD,∴K∈平面ABD,
同理K∈平面BCD,∴K∈BD。
說明:怎樣證明點在直線上?本題告訴我們,如果要證明點在兩個平面的交線上,那麼隻需要證明這個點既在第一個平面上又在第二個平面上即可。
【例2】證明:空間四邊形各邊的中點是平行四邊形的頂點。
提示設A₁,B₁,C₁和D₁是邊AB,BC,CD和DA的中點,則A₁B₁//AC和C₁D₁//AC,所以A₁B₁//C₁D₁(特别地,點A₁,B₁,C₁和D₁在一個平面上),類似地B₁C₁//A₁D₁。
【例3】證明:問題2中的平行四邊形的中心與連接四邊形對角線中點的線段的中點重合。
提示設A₁,B₁,C₁和D₁是邊AB,BC,CD和DA的中點。再設P和Q是對角線AC和BD的中點,則線段A₁Q和PC₁平行于線段AD,同時這兩個線段每一個的長等于線段AD長的一半,因此A₁PC₁Q是平行四邊形,所以線段A₁C₁的中點與線段PQ的中點重合。