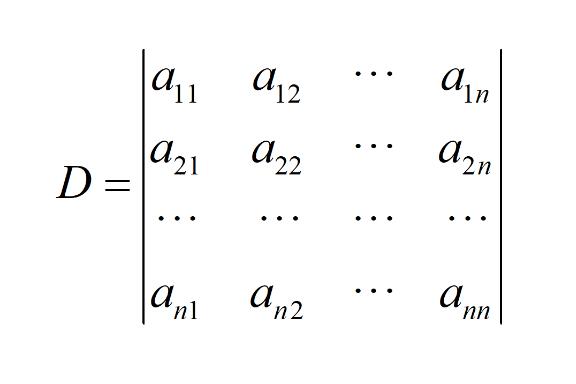基本介紹
一個n×n的方陣A的行列式記為det(A)或者|A|,一個2×2矩陣的行列式可表示如下:
把一個n階行列式中的元素aij所在的第i行和第j列劃去後,留下來的n-1階行列式叫做元素aij的餘子式,記作Mij。記Aij=(-1)i+jMij,叫做元素aij的代數餘子式。例如:
一個n×n矩陣的行列式等于其任意行(或列)的元素與對應的代數餘子式乘積之和;即:
相關定理
定理1設A為一n×n矩陣,則det(AT)=det(A)。
證對n采用數學歸納法證明。顯然,因為1×1矩陣是對稱的,該結論對n=1是成立的。假設這個結論對所有k×k矩陣也是成立的,對(k+1)×(k+1)矩陣A,将det(A)按照A的第一行展開,我們有:
det(A)=a11det(M11)-a12det(M12)+-…±a1,k+1det(M1,k+1),
由于Mij均為k×k矩陣,由歸納假設有
此式右端恰是det(AT)按照AT的第一列的餘子式展開。因此
定理2設A為一n×n三角形矩陣。則A的行列式等于A的對角元素的乘積。
根據定理1,隻需證明結論對下三角形矩陣成立。利用餘子式展開和對n的歸納法,容易證明這個結論。
定理3令A為n×n矩陣。
(i)若A有一行或一列包含的元素全為零,則det(A)=0。
(ii)若A有兩行或兩列相等,則det(A)=0。
這些結論容易利用餘子式展開加以證明。